Bentuk Aljabar adalah suatu bentuk matematika yang dalam penyajiannya memuat huruf-huruf untuk mewakili bilangan yang belum diketahui.
DAFTAR ISI
- Pengertian Bentuk Aljabar
- Operasi pada Bentuk Aljabar
- Penjumlahan dan Pengurangan pada Bentuk Aljabar
- Perkalian pada Bentuk Aljabar
- Pembagian pada Bentuk Aljabar
Pengertian Bentuk Aljabar
Pada bentuk aljabar terdapat unsur-unsur aljabar yang meliputi variabel, koefisien, konstanta, faktor, suku sejenis dan suku tidak sejenis.
Untuk lebih memahami Bentuk Aljabar, coba perhatikan tabel berikut.
Diasumsikan bahwa isi tiap dos adalah sama, begitu juga dengan tabung, akan tetapi kita tidak tau berapa banyak isi masing-masing dos dan tabung tersebut:
| No | Gambar | Bentuk Aljabar | Keterangan |
|---|---|---|---|
| 1. |  | 4 | 4 Bola |
| 2. |  | 2x + 2 | 2 Dos Bola dan 2 Bola |
| 3. |  | y + 3 | 1 Tabung Bola dan 3 Bola |
| 4. |  | 2x + y + 2 | 2 Dos Bola, 1 Tabung Bola, dan 2 Bola |
Dari ilustrasi diatas, terlihat bahwa ada berbagai macam bentuk aljabar.
Pada bentuk aljabar, terdapat beberapa istilah yang harus dikenal. Yaitu sebagai berikut:
Selain dari istilah diatas terdapat istilah lain yaitu suku satu (monomial), suku dua (binomial), suku tiga (Trinomial), suku Banyak (Polinomial), dan suku sejenis
Perhatikan Bentuk Aljabar dan suku-suku sejenis pada tabel berikut:
|
No. |
Bentuk Aljabar |
Suku-suku sejenis |
|
1. |
15x + 9y + 7x + 3y |
|
|
2. |
22x + 12y − 6x − 9y |
|
Operasi pada Bentuk Aljabar
Sema halnya dengan Operasi pada bilangan, pada bentuk aljabar juga terdapat sistem operasinya. yaitu:
- Operasi penjumlahan
- Operasi pengurangan
- Operasi perkalian
- Operasi pembagian.
Berikut ini diuraikan satu persatu:
Penjumlahan dan Pengurangan pada Bentuk Aljabar
Di dalam kehidupan sehari-hari banyak sekali masalah sehari-hari yang berkaitan dengan penjumlahan dan pengurangan bentuk aljabar.
Misalnya dalam dunia perbangkan, perdagangan di pasar, dan produksi suatu perusahaan.
Contoh:
Pak Madhuri merupakan seorang pemborong beras yang sukses di desa Dempo Timur. Pak Madhuri mendapatkan pesanan dari Pedagang pasar Pasean dan Waru di hari yang bersamaan. Pedagang pasar Pasean memesan 15 karung beras, sedangkan pedagang pasar Waru memesan 20 karung beras. Beras yang sekarang tersedia di gudang Pak Madhuri hanya 17 karung beras saja.
Misalkan x adalah massa tiap karung beras. Nyatakan dalam bentuk aljabar:
a. Total beras yang dipesan kepada Pak Madhuri.
b. Sisa beras yang ada di gudang Pak Madhuri jika memenuhi pesanan pedagang pasar Pasean saja.
c. Kekurangan beras yang dibutuhkan Pak Madhuri jika memenuhi pesanan pedagang pasar Waru saja.
Alternatif Pemecahan Masalah
a. Total beras yang dipesan kepada Pak Madhuri adalah 15x + 20x atau 35x kilogram beras.
b. Jika Pak Madhuri memenuhi pesanan pedagang pasar Pasean saja, maka sisa beras adalah 2 karung beras atau 2x kilogram beras.
c. Kekurangan beras yang dibutuhkan Pak Madhuri untuk memenuhi pesanan Pedagang pasar Waru adalah 3 karung beras atau (−3x) kilogram beras. (tanda negatif menyatakan kekurangan)
Pada cerita pengantar tersebut terdapat operasi antara dua bentuk aljabar, yaitu:
- Penjumlahan (15x) + (20x) = 35x
- Pengurangan (17x) − (15x) = 2x
- Pengurangan (17x) − (20x) = −3x
Bentuk 17x − 15x bisa juga ditulis penjumlahan dua bentuk aljabar 17x + (-15x)
Untuk mempelajari lebih lanjut tentang penjumlahan dan pengurangan bentuk aljabar, marilah kita amati dan lengkapi beberapa penjumlahan dan pengurangan bentuk aljabar pada Tabel berikut.
|
No. |
A |
B |
A + B |
B + A |
A – B |
B – A |
|
1. |
2x |
3x |
5x |
5x |
− x |
x |
|
2. |
x + 2 |
x + 7 |
2x + 9 |
2x + 9 |
− 5 |
5 |
|
3. |
x + 1 |
3x + 8 |
4x + 9 |
4x + 9 |
− 2x − 9 |
2x + 7 |
|
4. |
3x – 2 |
2x – 4 |
… |
… |
… |
… |
|
5. |
2x – 1 |
1 – x |
x |
x |
… |
… |
|
6. |
3x |
2x + 1 |
… |
… |
… |
… |
|
7. |
5 |
2x – 4 |
… |
… |
… |
… |
Contoh Aljabar dalam kehidupan sehari-hari
Perusahaan Z mengemas kelereng-kelereng ke dalam kotak-kotak, yaitu kotak merah dan kotak putih.
Wafi memiliki 15 kotak merah dan 9 kotak putih. Kotak-kotak tersebut berisi kelereng.
Jika banyak kelereng dikotak merah dinyatakan dengan x dan banyaknya kelereng di kotak putih dinyatakan dengan y, maka banyak kelereng di kedua kotak dinyatakan dengan 15x + 9y.
Keterangan:
- Banyak kelereng dalam setiap kotak merah sama.
- Banyak kelereng dalam setiap kotak putih sama.
Jika Wafi diberi kakaknya 7 kotak merah dan 3 kotak putih, maka Wafi sekarang mendapatkan tambahan kelereng sebanyak 7x + 3y.
Dengan demikian, Wafi sekarang memiliki (15x + 9y) + (7x + 3y) kelereng.
Bentuk (15x + 9y) + (7x + 3y) sama dengan 22x + 12y yang diperoleh dengan cara menjumlahkan kotak-kotak yang warnanya sama.
Bentuk (15x + 9y) + (7x + 3y) = 22x + 12y disebut Penjumlahan Bentuk Aljabar.
Karena Wafi memberikan 6 kotak merah dan 9 kotak putih kepada adiknya, maka kelereng yang dimiliki Wafi berkurang sebanyak 6x + 9y kelereng.
Dengan kata lain, kelereng yang dimiliki Wafi sekarang adalah (22x + 12y) − (6x + 9y) kelereng.
Bentuk ini sama dengan 16x + 3y yang diperoleh dengan cara mengurangkan kotak-kotak yang warnanya sama.
Bentuk (22x + 12y) − (6x + 9y) = 16x + 3y disebut Pengurangan Bentuk Aljabar.
Berikut disajikan beberapa contoh permasalahan tentang penjumlahan dan pengurangan dalam bentuk Aljabar.
Contoh 1
Tentukan penjumlahan 7a + 4b dengan 8a − 6b.
Alternatif Penyelesaian
(7a
+ 4b) + (8a − 6b)
= 7a + 4b + 8a + (–6b)
=
7a + 8a + 4b + (–6b)
= 15a + (−2b)
= 15a − 2b
Contoh 2
Tentukan pengurangan 7a + 4b oleh 8a − 6b.
Alternatif Penyelesaian
(7a + 4b) − (8a − 6b)
= 7a + 4b – 8a − (−6b)
= 7a − 8a + 4b + 6b
= −a + 10b
Contoh 3
Tentukan penjumlahan 16a − 12b + 4 oleh 5a − 9b + 2c.
Alternatif Penyelesaian
(16a −12b + 4) + ( 5a – 9b + 2c)
= 16a − 12b + 4 + 5a + (−9b) + 2c
= 16a + 5a − 12b − 9b + 2c + 4
= 21a − 21b + 2c + 4
Perkalian pada Bentuk Aljabar
Amati Masalah berikut:
Pak Idris mempunyai kebun apel berbentuk persegi dan Pak Tohir mempunyai kebun jeruk berbentuk persegi panjang. Ukuran panjang kebun jeruk Pak Tohir 20 m lebih dari panjang sisi kebun apel Pak Idris. Sedangkan lebarnya, 15 m kurang dari panjang sisi kebun apel Pak Idris. Jika diketah i kedua luas kebun Pak Idris dan Pak Tohir adalah sama, maka tentukan luas kebun apel Pak Idris?
Alternatif Pemecahan Masalah
Untuk memecahkan persoalan tersebut bisa dengan memisalkan panjang sisi kebun apel Pak Idris dengan suatu variabel, misal variabel x.
Panjang kebun jeruk Pak Tohir 20 meter lebih panjang dari panjang sisi kebun apel bisa ditulis x + 20.
Lebarnya 15 meter kurang dari panjang sisi kebun apel Pak Idris bisa ditulis x − 15.
Seperti yang kita ketahui bahwa luas persegi panjang adalah panjang × lebar.
Namun dalam permasalahan menentukan panjang sisi kebun tersebut, kita sedikit mengalami kesulitan karena yang dikalikan adalah bentuk aljabar.
Dalam permasalah tersebut luas kebun Pak Tohir adalah hasil kali dari x + 20 dengan x − 15.
Luas kebun Pak Tohir dapat ditulis dalam bentuk aljabar
Luas = panjang × lebar
= (x + 20) × (x − 15)
= x2 − 15x + 20x − 300
= x2 + 5x − 300
Selain dengan cara tersebut, kita bisa menentukan luas kebun Pak Tohir dengan cara perkalian bersusun seperti berikut.
(x + 20) x (x - 15)
= x2 + (-15)x + 20x + (-300)
= x2 + 5x - 300
Jadi, luas kebun Pak Tohir adalah x2 + 5x − 300 satuan luas.
Dari kedua cara tersebut, silakan menggunakan cara yang menurut kalian paling mudah.
Karena diketahui luas kebun apel Pak Idris sama dengan luas kebun jeruk Pak Tohir, maka didapat:
Luas kebun apel Pak Idris = Luas kebun jeruk pak Tohir
(x)2 = x2 + 5x – 300
x2 = x2 + 5x – 300
x2 – x2 = 5x – 300
0 = 5x – 300
5x = 300
x = 60
Jadi, luas kebun apel Pak Idris adalah (x)2 = (60)2 = 3.600 satuan luas.
Untuk lebih memahami tentang perkalian bentuk aljabar, amati perkalian bentuk-bentuk aljabar pada Tabel berikut. Kemudian lengkapi isi tabel yang masih kosong.
|
No. |
A |
B |
A × B |
Keterangan |
|
1. |
5 |
x + 10 |
5 × (x + 10) |
(5 × x) + (5 × 10) = 5x + 50 |
|
2. |
7 |
x - 3 |
7 × (x – 3) |
(7 × x) + (7 × (-3)) = 7x + (-21) = 7x – 21 |
|
2. |
4x |
x - 2 |
4x × (x – 2) |
(4x × x) + (4x × (-2)) = 4x2 + (-8x) = 4x2 - 8x |
|
3. |
x + 10 |
x + 3 |
(x + 10) × (x + 3) |
x × (x + 3) + 10 × (x + 3) = (x × x) + (x × 3) + (10 × x) + (10 × 3) = x2 + 3x + 10x + 30 = x2 + 13x + 30 |
|
4. |
x – 2 |
x + 7 |
……… |
|
Secara umur hasil perkalian bentuk aljabar (x + a) × (x + b) mengikuti proses berikut.
 |
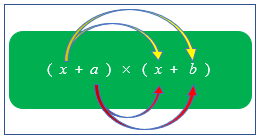| Dematika | Pola perkalian pada Bentuk Aljabar |
Mengenal Sifat-sifat Operasi Hitung Bentuk Aljabar
Operasi bentuk aljabar memenuhi beberapa sifat yang nantinya bisa memudahkan dalam menyelesaikan soal.
Adapun sifat-sifat aljabar adalah sebagai berikut.
1. Sifat komutatif
Sifat komutatif berlaku pada penjumlahan dan perkalian, yaitu sebagai berikut.
- a + b = b + a
- a × b = b × a
2. Sifat asosiatif
Sifat asosiatif berlaku pada penjumlahan dan perkalian, yaitu sebagai berikut.
- (a + b) + c = a + (b + c)
- (a × b) × c = a × (b × c)
3. Sifat distributif (Perkalian terhadap penjumlahan)
Sifat distributif adalah sifat yang meliputi operasi perkalian menjadi penjumlahan atau pengurangan.
- a × (b + c) = a × b + a × c atau a(b + c) = ab + ac
- a × (b – c) = a × b – a × c atau a(b – c) = ab – ac
Pembagian pada Bentuk Aljabar
Sepertihalnya perkalian, pembagian juga dapat dilakukan pada bentuk Aljabar.
Misalkan pada perkalian diatas, didapat sebagai berikut:
(x + 20) × (x − 15) = x2 + 5x – 300
Maka
(x2 + 5x – 300):(x + 20) = x − 15
Misalkan kita belum memiliki informasi sebelumnya, maka hasil dari (x2 + 5x – 300) dibagi dengan (x + 20), dapat dicari dengan cara sebagai berikut:
|
Langkah-langkah |
Pembagian bentuk aljabar (x2 + 5x – 300) ¸ (x + 20)= … |
Keterangan |
|
Langkah 1 |
 |
x2 + 5x – 300 dibagi x + 20. |
|
Langkah 2 |
 |
x2 dibagi x sama dengan x. |
|
Langkah 3 |
 |
x dikali x sama dengan x2 , x dikali 20 sama dengan 20x. |
|
Langkah 4 |
 |
x2 dikurangi x2 sama dengan 0, 5x dikurangi 20x sama dengan -15x. -300 dikurangan 0 sama dengan -300 |
|
Langkah 5 |
 |
-15x dibagi x sama dengan -15 |
|
Langkah 6 |
 |
-15 dikali x sama dengan x2 , -15 dikali 20 sama dengan -300. |
|
Langkah 7 |
 |
-15 dikurangi -15 sama dengan 0, -300 dikurangi -300 sama dengan 0. |
|
Jadi hasil bagi x2 + 5x – 300 oleh x + 20 adalah x − 15 |
||
Catatan:
Pada bentuk aljabar, pembagian tidak selalu bersisa 0.
Contoh :
Hasil bagi 2x2 + 3x − 4 oleh x + 3 adalah 2x – 3 dengan sisa 5.
Post a Comment